サクッとロジスティック回帰を試したい

ロジスティック回帰を使う時に、何を見れば良い。というのが自分の中でなかったので、まとめたいと思いました。

今回は、自分が、ロジスティック回帰を使う時に見るメモみたいな何かです。

scikit-learnでのパッケージ

ロジスティック回帰のパッケージは以下にあります。

from sklearn.linear_model import LogisticRegression

面白くないシンプルな例

ある未知のデータの発生源として尤もなのは、A/Bでどちらか？を求める例を考えます。

とりあえず、サンプルデータを作ります。

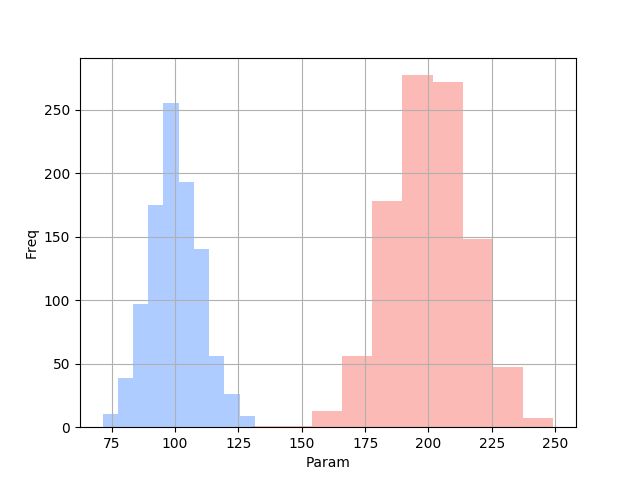
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

count = 1000

mean_A = 100
sigma_A = 10
mean_B = 200
sigma_B = 15

# 正規分布のデータを生成する
group_a= pd.Series(np.random.normal(mean_A, sigma_A, count))
group_b= pd.Series(np.random.normal(mean_B, sigma_B, count))

group_a.hist(color="#5F9BFF", alpha=.5)
group_b.hist(color="#F8766D", alpha=.5)

plt.xlabel("Param")
plt.ylabel("Freq")

plt.show()

こんなデータが正解データとしてあったとします。 データは完全に分離しているので、Paramの値を元にして、ロジスティック回帰で判定したら、確率が100%になるかなーというイメージで進めます。

ロジスティック回帰分析

サクッと、ロジスティック回帰分析を行います。

# Aグループを1にします. Bグループを2にします
group_a_y = pd.Series(np.full(group_a.size, 1))
group_b_y = pd.Series(np.full(group_b.size, 0))


# Logistic回帰に食わせるのにSeriesの１列にまとめた
X = pd.concat([group_a, group_b])
Y = pd.concat([group_a_y, group_b_y])

# 1次元しかない場合は、reshapeする必要がある
X = X.values.reshape(-1,1)

from sklearn.linear_model import LogisticRegression

log_model = LogisticRegression()
log_model.fit(X, Y)

# 予測精度（%)
print(log_model.score(X, Y)) # -> 100.0 %

ここまでで、ロジスティック回帰のモデルが出来上がりました。

100%分類できるモデルなので、あたり魔ですが、予測精度100%です。

次に、パラメータを渡して予測してみます。

>>> logi_model.predict(100)[0]
1
>>> logi_model.predict(120)[0]
1
>>> logi_model.predict(140)[0]
1
>>> logi_model.predict(160)[0]
0
>>> logi_model.predict(180)[0]
0
>>> logi_model.predict(200)[0]
0

140くらいまでは、1（グループA）で160から0（グループB）になっています。

想像通りなので、問題ないと思われます。

完全に分離できないパターン

次は完全に分離できないパターンを試してみます。

上記の例から、生成するデータの標準偏差を変えています。 また、予測結果は、判定後の結果ではなくて確率を出力しています。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

count = 1000

mean_A = 100
sigma_A = 30
mean_B = 200
sigma_B = 40

group_a= pd.Series(np.random.normal(mean_A, sigma_A, count))
group_b= pd.Series(np.random.normal(mean_B, sigma_B, count))

group_a.hist(color="#5F9BFF", alpha=.5)
group_b.hist(color="#F8766D", alpha=.5)

plt.xlabel("Param")
plt.ylabel("Freq")

plt.show()

# Aグループを1にします. Bグループを2にします
group_a_y = pd.Series(np.full(group_a.size, 1))
group_b_y = pd.Series(np.full(group_b.size, 0))


# Logistic回帰に食わせるのにSeriesの１列にまとめた
X = pd.concat([group_a, group_b])
Y = pd.concat([group_a_y, group_b_y])

# 1次元しかない場合は、reshapeする必要がある
X = X.values.reshape(-1,1)


from sklearn.linear_model import LogisticRegression

logi_model = LogisticRegression()
logi_model.fit(X, Y)

# 予測精度（%)
print("予測精度{}%".format(logi_model.score(X, Y) * 100))

def print_proba(param):
    print("Param is {}".format(param))
    result = logi_model.predict_proba(param)
    a = result[0][0] * 100
    b = result[0][1] * 100
    print("* グループA {}%".format(a))
    print("* グループB {}%".format(b))


for param in [70, 100, 130, 160, 190, 200]:
    print_proba(param)

出力されるグラフはこちら。

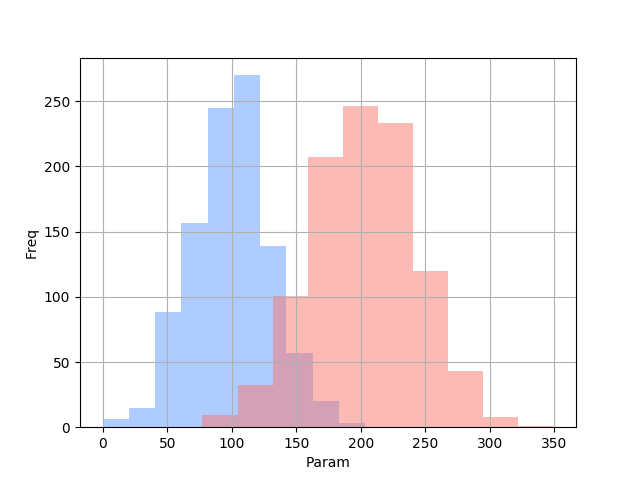
結果はこちら。

$ python sample_data2.py
予測精度92.55%
Param is 70
* グループA 0.7450809194575858%
* グループB 99.25491908054241%
Param is 100
* グループA 5.002287794157533%
* グループB 94.99771220584246%
Param is 130
* グループA 26.97362866157762%
* グループB 73.02637133842238%
Param is 160
* グループA 72.15243559131504%
* グループB 27.84756440868496%
Param is 190
* グループA 94.78480198275662%
* グループB 5.215198017243385%
Param is 200
* グループA 97.20601631423732%
* グループB 2.7939836857626785%

予測結果の確率と、グラフを見比べても良さげですね。

次は、パラメータの数を増やして試してみたいと思います。